Introduction
Lidar data is collected in the form raw mass points that
need to undergo processing steps in order to ensure they are accurate and
formatted properly to be used by the client. The processing steps are divided
into two parts; preprocessing and postprocessing. Geometric correction is an
important preprocessing step in which individual pixels are put into their
proper X, Y position. This lab is designed to provide experience with two
important types of geometric correction that are usually performed on satellite
images: image to map rectification and image to image registration.Both processes are done using Erdas Imagine.
Methods
Part 1: Image to Map Rectification
Image rectification is the process of converting data file coordinates to a map coordinate system through the creation of ground control points (GCPs) on the image to be rectified and a set in the same geographically positions on a reference map of the same area. The map coordinates of the GCPs are used to transform the image and produce a planimetric image. In this section of the lab a United States Geological Survey map of the Chicago metropolitan statistical area is used as a reference to rectify a Landsat TM image of the same area. In order to begin the process, two viewers must be open with the viewer containing the image to be rectified active. The interpolation process fits polynomials to the GCP data, the necessary order of the polynomial increases as the amount of distortion increases. As the order of the polynomial being applied increases, so does the number of GCPs necessary for the interpolation to run. The amount of distortion in the image provided for this section of the lab was not extensive so a first order polynomial was used and only three GCPs required, however four pairs will be placed. Until the minimum number of GCPs has been met each GCP pair must be manually placed in the same location on each image, subsequent GCPs only need to placed on one image and are automatically placed on the other image. After the minimum amount of GCPs have been created the status of the model changes from "has no solution" to "solution is current" and RMS values appear for each GCP. There is also a total RMS value at the bottom right of the screen. An ideal total RMS is less than 0.05; anything above 2.0 is too high and will not result in an accurate transformation. The goal for this section of the lab is 2.0 or less, which is achieve by zooming in on GCP pairs and placing them more accurately. The accuracy of all points must be verified, including the pairs with automatically placed counterparts. When an ideal RMS is achieved, the geometric correction process is ready to be run. The interpolation method can be changed to fit the correction being done, since the distortion in this image is low a simple nearest neighbor interpolation should result in an accurate correction. After the process has run, the resulting image is brought in and examined for accuracy.
Part 2: Image to Image Registration
In this section of the lab a corrected Landsat TM image of Sierra Leone is used as a reference to correct a distorted image of the same area. To assess the level distortion in the image it is brought into an Erdas viewer and the corrected reference image overlaid in the same viewer. At this point the viewer swipe can be used to swipe aside the reference image in either a vertical or horizontal direction to compare the images. In this case the level of distortion is quite high and will require a polynomial higher than a first order. For this example a third order polynomial will be necessary, requiring a minimum of ten GCPs. The correction process is the same as in part one except points one through ten will need to manually placed on both sides and then the model solution will become current. After the minimum of ten GCPs has been reached, two additional points will be placed. In this section of the lab the total RMS error will need to be 0.05 or below, this is achieved by meticulously examining each GCP pair and improving their accuracy. Due to the extent of distortion, when the correction process is ready to be run the interpolation method should be changed to one that results in a more spatially accurate image. The bilinear interpolation will be more suited to produce a more spatially accurate image from one with this level of distortion. With an ideal RMS error achieved and the proper interpolation method selected, the output image is highly accurate.
Results
Geometric correction is an important preprocessing step in the process of transforming Lidar raw mass points into an end product that can be used by the client. In this lab, the image to map rectification process has used map coordinate counterparts to rectify the pixel coordinates, resulting in a planimetric image (Figure 1). In this process the target RMS was quite difficult to reach, and after meticulous relocation of each GCP the RMS error remained around 1.89. The image to image to registration process used a similar procedure using a known corrected image to correct the distorted image. In the examples used in this lab,an ideal RMS error was much easier to obtain in the image to image registration process. Other than the spatial distortion, the images were exactly the same and it was possible to zoom into the same four pixels of each image and place the GCP at their intersection. This method resulted in a 0.00 RMS error after the first 10 GCPs were placed (firgure 2). Subsequent points beyond this increased the RMS as the automatically placed point were not as accurate. Correction of these inaccuracies resulted in a final RMS error of .2259 (figure 3).
Sources
Methods
Part 1: Image to Map Rectification
Image rectification is the process of converting data file coordinates to a map coordinate system through the creation of ground control points (GCPs) on the image to be rectified and a set in the same geographically positions on a reference map of the same area. The map coordinates of the GCPs are used to transform the image and produce a planimetric image. In this section of the lab a United States Geological Survey map of the Chicago metropolitan statistical area is used as a reference to rectify a Landsat TM image of the same area. In order to begin the process, two viewers must be open with the viewer containing the image to be rectified active. The interpolation process fits polynomials to the GCP data, the necessary order of the polynomial increases as the amount of distortion increases. As the order of the polynomial being applied increases, so does the number of GCPs necessary for the interpolation to run. The amount of distortion in the image provided for this section of the lab was not extensive so a first order polynomial was used and only three GCPs required, however four pairs will be placed. Until the minimum number of GCPs has been met each GCP pair must be manually placed in the same location on each image, subsequent GCPs only need to placed on one image and are automatically placed on the other image. After the minimum amount of GCPs have been created the status of the model changes from "has no solution" to "solution is current" and RMS values appear for each GCP. There is also a total RMS value at the bottom right of the screen. An ideal total RMS is less than 0.05; anything above 2.0 is too high and will not result in an accurate transformation. The goal for this section of the lab is 2.0 or less, which is achieve by zooming in on GCP pairs and placing them more accurately. The accuracy of all points must be verified, including the pairs with automatically placed counterparts. When an ideal RMS is achieved, the geometric correction process is ready to be run. The interpolation method can be changed to fit the correction being done, since the distortion in this image is low a simple nearest neighbor interpolation should result in an accurate correction. After the process has run, the resulting image is brought in and examined for accuracy.
Part 2: Image to Image Registration
In this section of the lab a corrected Landsat TM image of Sierra Leone is used as a reference to correct a distorted image of the same area. To assess the level distortion in the image it is brought into an Erdas viewer and the corrected reference image overlaid in the same viewer. At this point the viewer swipe can be used to swipe aside the reference image in either a vertical or horizontal direction to compare the images. In this case the level of distortion is quite high and will require a polynomial higher than a first order. For this example a third order polynomial will be necessary, requiring a minimum of ten GCPs. The correction process is the same as in part one except points one through ten will need to manually placed on both sides and then the model solution will become current. After the minimum of ten GCPs has been reached, two additional points will be placed. In this section of the lab the total RMS error will need to be 0.05 or below, this is achieved by meticulously examining each GCP pair and improving their accuracy. Due to the extent of distortion, when the correction process is ready to be run the interpolation method should be changed to one that results in a more spatially accurate image. The bilinear interpolation will be more suited to produce a more spatially accurate image from one with this level of distortion. With an ideal RMS error achieved and the proper interpolation method selected, the output image is highly accurate.
Results
Geometric correction is an important preprocessing step in the process of transforming Lidar raw mass points into an end product that can be used by the client. In this lab, the image to map rectification process has used map coordinate counterparts to rectify the pixel coordinates, resulting in a planimetric image (Figure 1). In this process the target RMS was quite difficult to reach, and after meticulous relocation of each GCP the RMS error remained around 1.89. The image to image to registration process used a similar procedure using a known corrected image to correct the distorted image. In the examples used in this lab,an ideal RMS error was much easier to obtain in the image to image registration process. Other than the spatial distortion, the images were exactly the same and it was possible to zoom into the same four pixels of each image and place the GCP at their intersection. This method resulted in a 0.00 RMS error after the first 10 GCPs were placed (firgure 2). Subsequent points beyond this increased the RMS as the automatically placed point were not as accurate. Correction of these inaccuracies resulted in a final RMS error of .2259 (figure 3).
 |
| Figure 1. Result of image-to-map rectification, rectified image on left and original on right |
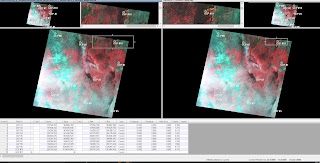 |
| Figure 2. A perfect RMS error after 10 GCPs had been added |
 |
| Figure 3. After 12 GCPs had been added the RMS was corrected to 0.2259, well within the ideal range |
Sources
Illinois Geospatial Data Clearing House. (n.d.).
Earth Resources
Observation and Science Center. (n.d.). United States Geological Survey.
Wilson, C. (2016). Lab
6: Geometric Correction. Eau Claire, WI, USA.
No comments:
Post a Comment